由于泵内部液体流动的复杂性，单凭借理论不能准确地算出叶片泵的性能，根据流体力学中的相似理论，并运用于实验模拟手段，可依泵叶轮在某一转速下的已知性能换算出它在其他转速下的性能。泵叶轮的相似定律是基于几何相似和运动相似的基础上的。凡是两台泵能满足几何相似和运动相似条件，称为工况相似泵。

几何相似条件是：两个叶轮主要过流部分一切相对应的尺寸成一定比例，所有的对应角相等。现设有两台几何相似泵的叶轮，一个为模型泵的叶轮，其符号以下角标“m”表示；另一个为实际泵的叶轮，其箱号不带下角标"m"。

则： b₂/b₂ₘ = D₂/D₂ₘ = λ （式56）

式中
b₂、b₂ₘ —— 分别为实际泵与模型泵叶轮的出口宽度；
D₂、D₂ₘ —— 分别为实际泵与模型耱叶轮的外径；
λ —— 任一线性尺寸的比例或称模型缩小的比例尺。例如比模型泵大一倍的实际泵 λ=2。

运动相似的条件是：两叶轮对应点上水流的同名速度方向一致，大小互成比例。也即在相应点上水流的速度三角形相似。所以，在几何相似的前提下，运动相似就是工况相似。

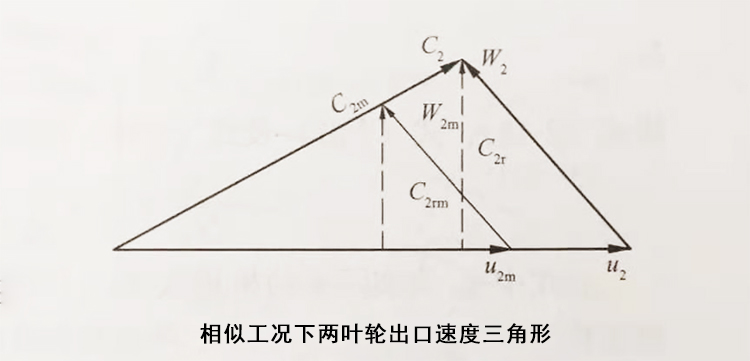
由上图可以得出：

C₂/C₂ₘ = u₂/u₂ₘ = nD₂/nₘD₂ₘ = λ·n/nₘ

也即：

C₂ᵤ/(C₂ᵤ)ₘ = C₂ᵣ/(C₂ᵣ)ₘ = u₂/(u₂)ₘ = D₂n/(D₂n)ₘ = λ·n/nₘ （式57）

叶轮相似定律有三个方面：

1、第一相似定律 —— 确定两台在相似工况下运行泵的流量之间的关系。

由式 ηᵥ = Q/Qₜ 即 Q = ηᵥF₂C₂ᵣ

所以 Q/Qₘ = ηᵥ/(ηᵥ)ₘ C₂ᵣ/(C₂ᵣ)ₘ F₂/(F₂)ₘ （式58）

因为 F₂ = πD₂b₂Φ₂

式中
Φ₂ —— 考虑叶片厚度而引起的出口截面减少的排挤系数，对于几何相似的叶轮，Φ₂ₘ = Φ₂ 。

对于两台满足相似条件的泵而言，将 式57 代入 式58 可得：

Q/Qₘ = λ³ · ηᵥ/(ηᵥ)ₘ · n/nₘ （式59）

式58 表示两台相似泵的流量与转速及容积效率的乘积成正比，与线性比例尺的三次方成正比。此式称为第一相似定律。

2、第二相似定律 —— 确定两台在相似工况下运行泵的扬程之间的关系。

由式 ηₕ = H/H'ₜ 可知，泵扬程 H = ηₕHₜ

也即 H = ηₕ/(1+p) · u₂C₂ᵤ/g

现假定表示反旋现象的修正系数 p 值相等。则：

H/Hₘ = ηₕu₂C₂ᵤ/(ηₕu₂C₂ᵤ)ₘ

因为，在相似工况下运行，故得：

H/Hₘ = λ² · ηₕn²/(ηₕn²)ₘ （式60）

上式表示两台相似泵的扬程与转速及线性比例尺的二次方及与水力效率的一次方成正比。此式称为第二相似定律。

3、第三相似定律 —— 确定两台在相似工况下运行泵的轴功率之间的关系。

因为 N= ρgQH/η

故 N/Nₘ = ρgQH/(ρgQH)ₘ · (η)ₘ/η

将式 η = ηₕ · ηᵥ · ηₘ 、式59、式60 代入上式，可得：

N/Nₘ = λ⁵ · η³/η³ₘ · (ηₘ)ₘ/(ηₘ) （式61）

式中
ηₘ —— 实际泵的效率；
(ηₘ)ₘ —— 为模型泵的效率。

抽升液体的密度相等时，式61表示了两台相似泵的轴功率与转速的三次方、线性比例尺的五次方成正比，与机械效率成反比。

实用中，如实际泵与模型泵的尺寸相关不太大，且工况相似时，可近似地认为三种局部效率都不随尺寸而变，则相似定律可写为：

Q/Qₘ = λ³ · n/nₘ （式62）

H/Hₘ = λ² · n²/n²ₘ （式63）

N/Nₘ = λ⁵ · n³/n³ₘ （式64）

 

点此回到目录：YILO 泵与泵站 技术专栏 - 目录

 

---

本专栏文章来自：中国建筑工业出版社-许仕荣《泵与泵站.第六版》；大连理工大学出版社-徐士鸣《泵与风机-原理及应用》；王圃、龙腾锐《给水泵站的水泵优选与节能改造》；金维、姜乃昌《停泵水锤及其防护》等文献。本站旨在泵与泵站技术的学习分享，非商业用途。我们致力于保护作者版权，如涉及侵权，敬请联系我们后台删除。