由离心泵的理论扬程公式：Hт = (u₂-C₂u)/g 中，将 C₂=u₂-C₂ᵣcotβ₂ 代入可得：

Hт = u₂/g(u₂-C₂ᵣcotβ₂) （式32）

叶轮中通过的流量可用下式表示：

Qт = F₂C₂ᵣ

也即

C₂ᵣ = Qт/F₂    （式33）

式中
Qт —— 泵理论流量（m³/h）。也即不考虑泵体内容积损失（如漏泄量、回流量等）的泵流量；
F₂ —— 叶轮的出口面积（m²）；
C₂ᵣ —— 叶轮出口处水流绝对速度的径向分速（m/s）。

将 式33 代入 式32 得：

Ht = u₂/g（u₂-Qт/F₂ · cotβ₂）    （式34）

式中 β₂、F₂ 均为常数。当泵转速一定时，u₂也为常数。故 式34 可以写成：

Ht = A-BQт     （式35）

式35 是一个直线方程式。当叶片的 β₂ < 90º时，也即叶片是后弯式时， Ht 将随 Qt 的增加而减小，如下图“离心泵的理论曲线”所示。该直线在纵坐标轴上的截距为 Hт = u₂²/g。

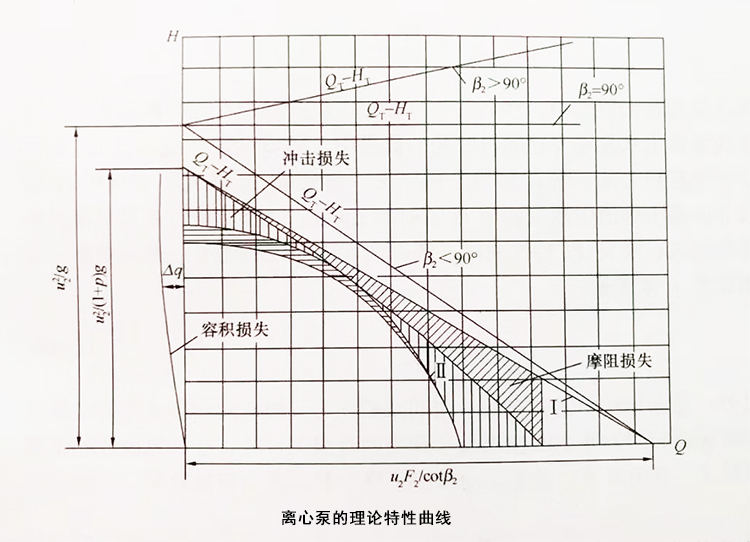
由 式16 “ H = ηhH'т = ηh（H'т/1+p）”可知，泵的理论扬程是需要进行修正的，首先考虑在叶槽中液流不均匀的影响，H'т = Hт/(1+p)，因此，在图“离心泵的理论曲线”上直线的纵坐标值将下降，成为直线 Ⅰ ，它与纵轴相交于 H'т = u₂²/(1+p)g。

其次，考虑泵内部的水头（扬程）损失，要从直线 Ⅰ上减去相应流量 Qт 下的泵内部水头损失，可得实际扬程 H 和理论流量 Qт 之间的关系曲线，也即 Qт-H 曲线（即曲线Ⅱ）。

离心泵内部的水头损失可分为两类：

（1）、摩阻损失等 Δh₁ ：在吸水室、叶槽中和压水室中产生的摩阻损失。其中包括转弯处的弯道损失和由流速头转化为压头的损失。其值可由下式表示：

Δh₁ = k₁Qт²      （式36）

式中
k₁ —— 比例系数。

（2）、冲击损失 Δh₂ ：泵在设计工况下运行时，可认为基本上没有冲击损失。当流量不同于设计流量时，在叶轮的进口导水器、蜗壳压水室的进口等处就会发生冲击现象。流量与设计值相差越远，冲击损失也越大。其值可用下式表示：

Δh₂ = k₂（Qт-Q₀）²      （式37）

式中
Q₀ —— 设计工况点的流量（m³/h）；
k₂ —— 比例系数。

泵体内这两部分水力损失必然要消耗一部分功率，使泵的总效率下降。其值可用水力效率 ηₕ 来度量：

ηₕ = H/H'т      （式38）

在对离心泵构造的讨论中，我们知道：在泵工作过程中存在着泄漏和回流问题，也就是说泵的出水量总要比通过叶轮的流量小，即 Q = Qт-Δq，此 Δq 就是渗漏量，它是能量损失的一种，称为容积损失。渗漏量 Δq 值大小与扬程 H 有关。从曲线 Ⅱ 的横坐标值中减去相应 H 值时的 Δq 值，这样就可最后求得扬程随流量而变化的离心泵 Q-H 特性曲线。考虑到容积损失消耗了一部分功率，其值可用容积效率 ηᵥ 来度量：

ηᵥ = Q/Qт      （式39）

除此以外，泵在运行中还存在轴承内的摩擦损失、填料轴封装置内的摩擦损失以及叶轮盖板旋转时与水摩擦损失（称为圆盘损失）等，这些机械性的摩擦损失同样消耗了一部分功率，使泵的总效率下降。其值可用机械效率 ηₘ 来度量：

ηₘ = Nₕ/N      （式40）

式中
Nₕ —— 叶轮传给水的全部功率，称为水功率（N=ρgQтH'т）。也即是，泵轴上输入的功率只有在克服了机械摩阻以后，才把剩下的功率传给了液体。

因此，由泵的效率公式得知，泵的总效率 η 为：

η = Nᵤ/N = ρgQH/N

即

η = ρgQH/ρgQH'т · ρgQH'т/ρgQтH'т · ρgQтH'т/N

将 式38、式39、式40 代入上式，即得：

η = ηₕ · ηᵥ · ηₘ       （式41）

由 式41 可看出，泵的总效率 η 是3个局部效率的乘积。要提高泵的效率，必须尽量减少机械损失和容积损失，并力求改善泵壳内过水部分的设计、制造和装配，以减少水力损失。

由以上对于 Q-H 特性曲线的理论分析中，可以知道，如果用分析方法来求特性曲线，必须计算泵内的各种损失。然而，这是很难精确计算的。因此，一般水泵厂都采用实验的方法来实测泵的性能曲线。以上的定性分析，虽然最终未能解决泵实用上的数值问题，但它却从物理概念上作出了比较清楚的说明。

另外，由 式34 可知，当 β₂>90º 时，刚：

Hт = A+BQт       （式42）

另外，由 式42 可看出，泵的扬程将随流量的增大而增大，并且，它的轴功率也将随之增大。对于这样的离心泵，如使用于城市给水管网中，将发现它对电动机的工作是不利的。因为，城市给水管网的工作流量是很不均匀的，对中小城市来讲，昼夜间用水量的变化幅度是比较悬殊的，特别是遇到消防或干管断裂等情况，其流量的变化幅度就更大，这时，如果采用的是 β₂>90º 的叶轮，则泵的轴功率也将在一个相当大的幅度内变化着，它将要求电动机能在很大的功率变化范围内有效地工作，这对一般的电动机是有困难的。另外，式42 也仅仅是理论上的。

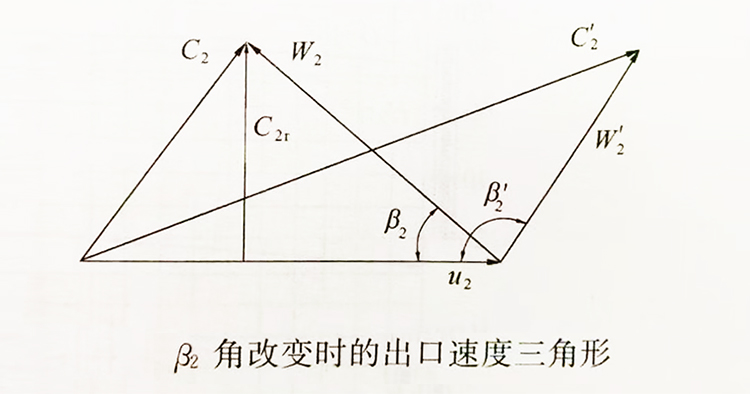
实际上，从上图“β₂角改变时的出口速度三角形”中可以看出：当泵转速 n 和流量 Q 一定时，则圆周速度 u₂ 就一定，绝对速度的径向分速 C₂ᵣ 也就一定，当 β₂ 增大时，出口的绝对速度 C₂ 就增大。结果，换得的只是叶轮出口的动能增大，它使叶轮出口的蜗壳内的水头损失增加，最后，这种动扬程 H₂ 的增加，将无法被有效地利用。

再则，为了避免在叶轮进口处产生旋涡，目前，一般离心泵叶轮的进口 α₁ 采用 90º，这样，如果 β₂ 采用大于 90º 时，叶片的形状在几何上必然会加大流槽的弯度，整个叶片存在有方向不同的两个弯曲，使叶轮内流体的弯道损失加大。

所以，权衡利弊，目前离心泵的叶轮几乎一律采用了后弯式叶片（β₂=20º~30º左右）。这种形式叶片的特点是随扬程增大，泵流量减小，因此，其相应的流量 Q 与轴功率 N 关系曲线 （Q-N曲线），也将是一条比较平缓上升的曲线，这对电动机来讲，可以稳定在一个功率变化不大的范围内有效地工作。

 

点此回到目录：YILO 泵与泵站 技术专栏 - 目录

 

---

本专栏文章来自：中国建筑工业出版社-许仕荣《泵与泵站.第六版》；大连理工大学出版社-徐士鸣《泵与风机-原理及应用》；王圃、龙腾锐《给水泵站的水泵优选与节能改造》；金维、姜乃昌《停泵水锤及其防护》等文献。本站旨在泵与泵站技术的学习分享，非商业用途。我们致力于保护作者版权，如涉及侵权，敬请联系我们后台删除。